Teorema de Bell

Teorema de Bell: Uma Visão Geral com Links Lotsa

Tradução automática realizada em 7 de outubro de 2022

Por David R. Schneider
www.DrChinese.com
NOTA: Por favor, sinta-se à vontade para criar um link para esta página. Vou deixá-lo permanentemente para este fim.


JS Bell
Nesta página:

Visão geral:
Introdução
Histórico
Polarização de fótons
Emaranhamento
Suposições que levam à Desigualdade
de Bell Testes da

Desigualdade de Bell Nota: A visão geral destina-se aos novatos neste assunto. Leitores avançados se beneficiarão dos links.

Categorias de links:
Mais sobre Bell do DrChinese
Bell's Theorem
Tests of Bell's Inequality
O Teorema GHZ e outros teoremas que excluem o Realismo Local
Multifótons e outros Emaranhamento Exótico
Parametric Down Conversion (PDC), o Quantum Eraser e outros fenômenos físicos
Stanford/Wikipedia adicional /Referências do site Nobel de interesse
Discussão filosófica e outras sobre o Teorema de Bell

Nota: Os links incluem muitos artigos acadêmicos (avançados), bem como referências introdutórias/intermediárias... algo para todos!


VISÃO GERAL:

Introdução

O Teorema de Bell é o legado do falecido grande JS Bell. Publicado em 1965, o Teorema de Bell é famoso por traçar uma importante linha na areia entre a Mecânica Quântica (QM) e o mundo como o conhecemos intuitivamente. É simples e elegante e, ao mesmo tempo, aborda muitas das questões filosóficas fundamentais relacionadas à física moderna. Se você quiser entender o significado mais rico da Relatividade e da Teoria Quântica, também vai querer aprender sobre Bell. Em sua forma mais simples, o Teorema de Bell afirma:

Nenhuma teoria física de Variáveis ​​Ocultas locais pode reproduzir todas as previsões da Mecânica Quântica.

O significado desta afirmação é o seguinte: A Mecânica Quântica é a teoria "estranha" introduzida em 1927 por Niels Bohr e Werner Heisenberg para descrever a natureza fundamental das partículas básicas: o núcleo atômico, elétrons e luz (fótons ou ondas eletromagnéticas). Esta teoria foi uma tremenda melhoria em relação à teoria pré-existente, e rendeu sucessos imediatos. De fato, a mesma teoria existe hoje como Mecânica Quântica sem praticamente nenhuma mudança (embora tenha sido estendida para explicar mais fenômenos). A versão de 1927 introduziu novos conceitos como: o Princípio da Incerteza de Heisenberg; interpretação estatística de Max Born da função de onda, incluindo superposição; e complementaridade de Bohr (dualidade onda-partícula). Além disso, inclui importantes avanços recentes como a função de onda de Schoedinger (1925); o princípio de exclusão de Pauli (1923); o modelo semi-clássico do átomo de Bohr (1913); contribuições adicionais de Louis de Broglie e Paul Dirac; e, claro, o trabalho seminal inicial de Max Planck (1900) e Albert Einstein (1905).

Então qual é o problema? Por que discutir com o sucesso? A resposta é que as implicações filosóficas da nova Teoria Quântica eram preocupantes para muitos físicos proeminentes da época, incluindo o próprio Albert Einstein. Eles sentiram que a Teoria Quântica poderia ser um trampolim, mas não poderia ser uma teoria final. E assim começou uma longa série de ataques à teoria nascente. Einstein e outros achavam que as falhas na QM eram óbvias, mas a teoria não mostrava fraquezas em sua capacidade de fazer previsões úteis. Bohr era o defensor do QM: se estava errado, por que suas previsões estavam certas? Então, foi argumentado que a teoria não era realmente "errada", mas sim "incompleta". No entanto, não houve modificações significativas. O Teorema de Bell mostra que o sonho de uma teoria "mais completa" é apenas isso: um sonho. Isso não pode acontecer. Que um único teorema (e elegantemente direto) pudesse encerrar um debate tão importante é o que levou Stapp a chamar esse teorema de "o mais profundo da ciência" (1975).

Esta página destina-se a fornecer uma visão geral do Teorema de Bell: a história, uma breve explicação e um resumo dos testes do Teorema de Bell. Além disso, você encontrará muitos links para assuntos intimamente relacionados ao Teorema de Bell.


História

Em 1935, Albert Einstein colaborou com Boris Podolsky e Nathan Rosen para publicar um artigo que agora é simplesmente referido pelas iniciais de seus três autores: EPR (1). Em essência, eles concluíram que a Mecânica Quântica estava incompleta porque existiam as chamadas "Variáveis ​​Ocultas" que devem explicar pelo menos algumas das incertezas presentes na QM. Variáveis ​​Ocultas significa que existem propriedades microscópicas de partículas fundamentais que não podemos observar diretamente por meio de testes, talvez devido a limitações tecnológicas que podem não existir em algum momento futuro. Ou seja, talvez simplesmente precisemos de um microscópio maior para ver os detalhes do que está acontecendo no menor nível. Mas como não podemos observá-los, eles podem estar "escondidos"

O EPR tinha uma definição simples, mas poderosa, do que eles chamavam de "elemento da realidade": SE uma propriedade observável de um sistema pudesse ser prevista com absoluta certeza (100%) sem perturbar esse sistema, ENTÃO ela deveria corresponder a um elemento da realidade. Uma definição simples e sucinta, com certeza. E um com o qual poucos discutiriam.

EPR forneceu uma prova que diz em essência: ou existem Variáveis ​​Ocultas, OU atributos de partículas (como posição, velocidade, energia, polarização, etc.) não são reais e definidos até que sejam observados. EPR também disse que, uma vez que é "irracional" acreditar que esses atributos de partículas requerem observação para se tornarem reais, portanto, Variáveis ​​Ocultas devem existir. Einstein disse: "Eu acho que uma partícula deve ter uma realidade separada independente das medidas. Ou seja: um elétron tem spin, localização e assim por diante mesmo quando não está sendo medido. Eu gosto de pensar que a lua está lá mesmo se Eu não estou olhando para isso." (É claro que esta declaração não pretende ser um ponto literal de debate.)

Bell viu isso de forma diferente, como muitos físicos fizeram, e concluiu que não havia Variáveis ​​Ocultas Locais. Ou seja, o que é "irracional" é simplesmente uma questão de opinião, e não é uma prova definitiva. QM realmente diz que uma observação molda a realidade - e pode fazê-lo mesmo depois do fato! Uma posição estranha, com certeza, mas não contrariada pelos fatos. (Nota: Se você estiver interessado, esta parte do QM é chamada de Princípio da Incerteza de Heisenberg.) Partindo dessa posição, Bell então foi além: ele mostrou que os cenários de Variáveis ​​Ocultas Locais impõem um requisito crítico que não é óbvio. 30 anos após o EPR, Bell expôs esse requisito. Ela é chamada de Desigualdade de Bell e pode ser testada experimentalmente usando partículas emaranhadas. A física é descrita abaixo, e os resultados são descritos.


Polarização do fóton

Vamos considerar o caso da polarização da luz. Esta é a maneira mais fácil de se relacionar com o Teorema de Bell (embora seu teorema esteja realmente relacionado ao spin do elétron, que é muito semelhante).

Uma partícula de luz é chamada de fóton (isso é exatamente o mesmo que uma onda eletromagnética; as ondas de rádio são, na verdade, fótons). A maioria dos fótons são polarizados linearmente e essa polarização pode ser observada (medida) usando um filtro polarizador ou um cristal polarizador. Os óculos de sol polarizadores utilizam esta característica de polarização como base para o seu funcionamento. Como regra geral, metade de toda a luz polarizada ALEATÓRIA passará por um filtro polarizador. A outra metade será refletida/absorvida pelo filtro. Isso é verdade independentemente da orientação do filtro. Geralmente, o filtro pode ser ajustado em qualquer ângulo de 0 graus a 360 graus - ou seja, pode ser girado à vontade em um círculo. Esses efeitos são vistos mesmo que a fonte de luz seja tão fraca que um único fóton passe por ela de cada vez!  Uma vez que qualquer fóton passe através de uma lente polarizadora, sua polarização será alinhada exatamente com a lente a partir de então (mesmo que não tenha sido anteriormente).

Suponha que consideremos uma única partícula (fóton) de luz. Fazemos uma pergunta simples: ele tem uma polarização definida nos três ângulos a seguir: 0 graus (A), 120 graus (B) e 240 graus (C)? De acordo com o artigo da EPR, sua polarização nesses 3 ângulos corresponde a elementos reais da realidade SE eles puderem ser previstos com certeza sem perturbar o sistema. Isso pode ser confirmado através da óptica convencional: qualquer fóton com uma polarização conhecida (digamos 0 graus) pode ser verificado posteriormente por outro polarizador na mesma configuração de ângulo. O resultado previsto (100% de certeza) é que o fóton terá a mesma polarização naquele momento posterior, e isso é conhecido há cerca de 200 anos (Malus, 1809). Por extensão, A, B e C devem corresponder individualmente aos elementos da realidade, conforme definição de EPR.

Em seguida, chegamos à pergunta de $ 64.000: A, B e C correspondem a elementos SIMULTÂNEOS da realidade? De acordo com EPR, um elemento de realidade existe independente do ato de observação. IE todos os elementos da realidade têm valores definidos em todos os momentos, MESMO QUE NÃO SABEMOS SEUS VALORES. Na verdade, a EPR diz que qualquer outra posição não seria razoável. Assim, de acordo com essa visão, os ângulos A, B e C devem ter respostas definidas simultâneas para as questões de suas polarizações - mesmo que não possam ser conhecidas. Assim, no ângulo A pode haver uma variável oculta A; e no ângulo B ocultamos a variável B; e, no ângulo C, ocultamos a variável C. Se ao menos tivéssemos as ferramentas, talvez pudéssemos aspirar algum dia a observar simultaneamente as variáveis ​​ocultas A, B e C de um único fóton.

The $ 64.000 Question foi um game show americano transmitido em horário nobre na CBS-TV de 1955 a 1958, que se envolveu nos escândalos do programa de perguntas e respostas da década de 1950 . Os participantes responderam a perguntas de conhecimentos gerais, ganhando dinheiro que dobrou à medida que as perguntas se tornaram mais difíceis. A pergunta final teve um prêmio principal de US$ 64.000 (equivalente a US$ 650.000 em 2021), daí a "Pergunta de US$ 64.000" no título do programa.

Emaranhamento

Bell estava ciente de que havia alguns casos incomuns em que pares de partículas poderiam ser criados que tinham uma propriedade incomum - eles permaneceram conectados de alguma forma mesmo depois de separados. Essa conexão é chamada de emaranhamento. Esse par de partículas atua como um sistema até o momento em que uma medição é realizada em uma ou na outra. Quando um é observado, o outro imediatamente assume um estado compatível com uma regra de conservação aplicada ao par como um sistema combinado. Isso acontece mesmo se a distância entre o par for muito grande para ser contabilizada por um sinal normal viajando na velocidade da luz entre as partículas (ou seja, de uma para a outra). Uma influência mais rápida que a luz poderia violar a relatividade - no entanto, verifica-se que não há como usar esse "efeito" para realizar qualquer tipo de sinalização.

O emaranhamento é a chave para testar o Teorema de Bell. Um par de partículas emaranhadas pode se separar, indo em direções opostas. A orientação real do spin do par não é conhecida. O que se sabe é a relação entre os dois. Em uma configuração típica, se o giro de um é "vertical", o giro do outro é "horizontal" (e vice-versa). Isso é conhecido como spins ortogonais (ou perpendiculares).


Suposições que levam à Desigualdade de Bell

Voltando à questão dos "$64.000" sobre a existência simultânea de A, B e C: o Teorema de Bell aborda isso matematicamente usando partículas emaranhadas como sua base. Para ver o tratamento matemático, O próprio artigo original de Bell em formato PDF. A matemática é ignorada aqui e, em vez disso, "vamos direto ao ponto", por assim dizer.

Bell viu três suposições que ele achava que qualquer teoria realista local incluiria, independentemente de sua natureza:

1. Ela deveria concordar com as previsões da Mecânica Quântica (de modo a concordar com experimentos estabelecidos).
2. Deve seguir os princípios da relatividade (as causas não podem se propagar mais rápido que a velocidade da luz) - isso é chamado de Localidade (às vezes, Localidade de Bell). Especificamente, uma configuração de medição para um membro de um par de partículas emaranhadas não deve afetar os resultados de uma medição no outro membro do par localizado à distância. Caso contrário, você teria a chamada "ação assustadora à distância".
3. Deve haver existência simultânea dos elementos da realidade descritos acima (A, B e C, por exemplo). Isso é frequentemente chamado de "Variáveis ​​Ocultas" ou às vezes "Realismo".

Uma pessoa que acredita nas suposições 2. e 3. acima é chamada de Realista Local. Essas duas suposições são muito razoáveis, e muitos físicos acreditaram nelas antes de Bell. Por que não? Você simplesmente aceitou as previsões de QM e assumiu que 2. e 3. também eram verdadeiras. Mas... Bell mostrou que as três suposições acima são realmente incompatíveis quando combinadas. Portanto, pelo menos um deve estar errado. Bell derivou uma previsão testável específica relacionada a isso chamada Desigualdade de Bell. Se a Desigualdade de Bell estiver correta, então a primeira suposição está errada. Esta foi a linha na areia para o Realista Local.


Testes da Desigualdade de Bell

Os Testes da Desigualdade de Bell são comumente chamados de testes do Paradoxo EPR, ou simplesmente testes de Bell. Se a Desigualdade de Bell for violada (ou seja, incorreta), então deve ser a segunda ou a terceira suposição acima que é violada. Os experimentos de Alain Aspect (*1) et al, especialmente os testes de 1981 usando analisadores variantes no tempo, mostraram que a desigualdade IS de Bell foi violada e as previsões de QM foram suportadas. Portanto, ou a natureza é não local ou não há variáveis ​​ocultas. De qualquer forma, a posição realista local está agora desacreditada. Não há possibilidade de uma futura teoria Realista Local que concorde com QM.

(*)Premio Nobel de Física 2022

Os primeiros testes estabeleceram um padrão que está sendo aprimorado até hoje. Testes repetidos de partículas emaranhadas continuam a demonstrar que a Desigualdade de Bell é violada com precisão estatística cada vez maior. Testes recentes envolvem inúmeras variações, melhorias e eficiências aprimoradas. Eles apóiam a Mecânica Quântica e rejeitam as teorias do Realismo Local com mais de 30 desvios padrão - uma conquista incrível. A pesquisa continua na compreensão da verdadeira natureza do emaranhamento de partículas.







LINKS: Teorema de Bell [retornar ao índice do link superior] • Esta é uma apresentação de alto nível do Teorema de Bell, tratamento muito abrangente por um dos pioneiros do campo: Abner Shimony: "Teorema de Bell" , Platão de Stanford (atualizado em 2005) • A visão geral de Mermin do Teorema de Bell cobre muito terreno (.PDF, 267k): N. David Mermin: "A lua está lá quando ninguém olha? A realidade e a teoria quântica" , Physics Today (abril de 1985) • Este é um grande apresentação do EPR Paradox: Arthur Fine: "The Einstein-Podolsky-Rosen Argument" , Platão de Stanford (atualizado em 2004) • Uma recapitulação do atual "estado do debate" , do próprio Alain Aspect (.PDF):

Aspect: "Teste de desigualdade de Bell: mais ideal do que nunca" (PDF) , Nature (2001)

• Uma recapitulação do Teorema de Bell na Scholarpedia - observe que isso é escrito a partir de uma
perspectiva Bohmiana (mecânica não local) e não segue inteiramente protocolos padrão sobre o assunto:
Goldstein, Norsen, Tausk, Zanghi: "Teorema de Bell" , Scholarpedia (2011)


Testes da Desigualdade de Bell [voltar ao topo do índice do Link]

• O Experimento de Innsbruck de 1998 (EPR com 1 quilômetro de separação) é o padrão-ouro dos testes de Bell:
Weihs, Jennewein, Simon, Weinfurter e Zeilinger: Violation of Bell's Desigualdade sob estrita localidade de Einstein condições (PDF)

• Teste de Bell que fecha a lacuna de amostragem justa:
Rowe, Kielpinski, Meyer, Sackett, Itano, Monroe, & Wineland: violação experimental de uma desigualdade de Bell com detecção eficiente (PDF), Nature, 1998.

• Testes de Bell são agora sendo feito no nível de graduação:
Dietrich Dehlinger e MW Mitchell: Fótons entrelaçados, não localidade e desigualdades de Bell no laboratório de graduação (PDF), American Journal of Physics, 2002.

• Revisão abrangente dos testes de Bell a partir de 2006 (com 505 referências):
Marco Genovese: Research on Hidden Variable Theories: a review of recent progresses , arXiv, 2007.


Mais sobre Bell do DrChinese [retornar ao índice do link superior]

• A prova mais curta do mundo (e garantidamente mais simples!!) do Teorema de Bell:
David Schneider: Teorema de Bell com Matemática Fácil

• Derivação do Teorema de Bell demonstrando que probabilidades negativas são uma consequência paradoxal:
David Schneider: Teorema de Bell e Probabilidades Negativas

• Os artigos originais que dizem tudo:
David Schneider: EPR, Bell & Aspect: The Original References (em formato PDF)

O Teorema GHZ, e outros teoremas que excluem o Realismo Local [retornar ao topo do índice do link]

• O importante Teorema GHZ (1989) é difícil de localizar no original, aqui está o melhor que tenho para você:
"experiência GHZ", Wikipedia

• A realização do Teorema GHZ experimentalmente, infelizmente não é gratuita:
"Teste experimental de não-localidade quântica no emaranhamento de três fótons de Greenberger-Horne-Zeilinger", Pan, Bouwmeester, Daniell, Weinfurter & Zeilinger (2000)

• Testes experimentais do Teorema GHZ usando 3 fótons, que inclui a discussão do teorema na seção 16.2 (.PDF):
J. Pan e A. Zeilinger: Multi-Photon Entanglement and Quantum Nonlocality, do livro Quantum [Un]Speakables. Do Teorema de Bell à Informação Quântica, R. Bertlmann, A. Zeilinger, editores, (2002).

• O Paradoxo de Hardy é testado como forma de descartar o realismo local (.PDF):
Carlson, Olmstead e Beck: Mistérios quânticos testados

• Outra contradição com o realismo local:
Carston Held: O Teorema de Kochen-Specker , Platão de Stanford

• Realização experimental do acima, descartando teorias não contextuais:
Bartosik, Klepp, Schmitzer, Sponar, Cabello, Rauch, Hasegawa: teste experimental de contextualidade quântica em interferometria de nêutrons , (2009)

• Realização experimental do Paradoxo de Hardy, também descartando teorias realistas:
Yokota, Yamamoto, Koashi e Imoto: Observação direta do paradoxo de Hardy por medição fraca conjunta com um par de fótons emaranhados , New Journal of Physics (2009)

• Teorema de Leggett mostra as limitações descrevendo o passado não observado de uma partícula:
Bacciagaluppi: Teorema de Leggett sem desigualdades , Fundamentos de Probabilidade e Física 5 (2008)

Emaranhamento de multifótons e outros exóticos [voltar ao topo Índice de links]

• Dois não é o limite para partículas emaranhadas:
Eibl, Gaertner, Bourennane, Kurtsiefer, Zukowski, Weinfurter: Observação experimental de emaranhamento de quatro fótons a partir de conversão descendente, Revisão Física Cartas (2003)

• Emaranhado Emaranhado:
P. Walther, K. Resch, C. Brukner, A. Zeilinger: Emaranhado Emaranhado Experimental

• Hiperemaranhamento:
Julio Barreiro: Fótons Hiperemaranhados


Parametric Down Conversion (PDC), o Quantum Eraser e outros fenômenos físicos [retornar ao topo Índice de links]

• Usando uma configuração EPR para demonstrar a natureza da partícula da luz em uma configuração de mesa relativamente barata (repetindo um experimento realizado pela Aspect e outros) (.PDF):
Thorn, Neel, Donato, Bergreen, Davies e Beck : Observando o comportamento quântico da luz em um laboratório de graduação (PDF), American Journal of Physics (2002)

• Uma discussão sobre borrachas quânticas (.PDF):
Herzog , Kwiat, Weinfurter, Zeilinger: Complementarity and the Quantum Eraser, Physical Review Letters (1995)

Referências adicionais de interesse do site Stanford/Wikipédia/Nobel [retornar ao início do índice do link]

• Para saber mais sobre o emaranhamento quântico:
Jeffry Bub: "Quantum Entanglement and Information", Platão de Stanford (atualizado em 2001)

• Ótima perspectiva histórica:
Jan Faye : "A Interpretação de Copenhague", Platão de Stanford (atualizado em 2002)

• Discussão da Wikipedia sobre o Teorema de Bell:
Vários: "Teorema de Bell", Wikipedia

• Discussão da Wikipedia sobre experimentos de teste de Bell:
Vários: "Experimentos de teste de Bell", Wikipedia

• Para o descoberta da constante de Planck:
Max Planck:, site Nobel

• Pela lei do efeito fotoelétrico:
Albert Einstein: "O Prêmio Nobel de Física, 1921" , site Nobel

• Pela estrutura do átomo de hidrogênio e radiação quantizada:
Niels Bohr: "O Prêmio Nobel de Física, 1922 " , site Nobel

• Por sua descrição do elétron como partícula e onda:
Louis De Broglie: "O Prêmio Nobel de Física, 1929" , site Nobel

• Pela descoberta do Princípio da Incerteza de Heisenberg e invenção da Teoria Quântica:
Werner Heisenberg: "O Prêmio Nobel de Física, 1932" , site Nobel

• Por suas contribuições:
Schoedinger e Dirac: "O Prêmio Nobel de Física, 1933" , site Nobel

• Pelo Princípio de Exclusão de Pauli:
Wolfgang Pauli: "O Prêmio Nobel de Física, 1945" , site Nobel

• Pela interpretação estatística da função de onda:
Max Born : "O Prêmio Nobel de Física, 1954" , site Nobel

Discussão Filosófica e Outras sobre o Teorema de Bell e Testes Experimentais [retornar ao topo Índice do Link]

• O que é "Localidade de Bell"? Isso explica, além de definições para Independência de Parâmetro e Independência de Resultado:
Travis Norsen: EPR e Bell Locality, arXiv (2005)

• A interferência está relacionada à incerteza:
Thomas Marcella: interferência quântica com fendas, European Journal of Physics (2002)

(c) 2005-2009 David Schneider/DrChinês
NOTA: Sinta-se à vontade para criar um link para esta página.

Postagem complementar, relativa ao Prêmio Nobel de Física de 2022
https://fisica2100.forumeiros.com/t599-entrelacamento-quantico#13832

Página Original, em Inglês
https://www.drchinese.com/Bells_Theorem.htm

Teorema de Bell em video em castelhano.



Uma tentativa de explicar o teorema de Bell aos pobres mortais.

"Cale a Boca e Calcule!" Assim dizia Feynman.

Como aceitar as "verdades" propaladas pela física quântica?

1 - Admitir que somos suficientemente burros para jamais entender os "fundamentos" mecânica quântica;

2 - Acreditar que os físicos quânticos testaram o Teorema de Bell sem dados viciados, de modo que foram capazes de provar uma negativa;

3 - Acreditar que o átomo é uma máquina ideal, capaz de funcionar sem uma fonte de energia externa.

Jonas Paulo Negreiros escreveu:
1 - Admitir que somos suficientemente burros para jamais entender os "fundamentos" mecânica quântica;

Isto é verdade, se não podermos aceitar que existe o multiverso

Uma hipótese absurda para entender o efeito fantasmagórico a longa distância é exatamente duvidar que existe a dimensão "distância".

Todo universo operaria dentro de um único ponto adimensional. Isso "resolveria" a comunicação instantânea de um único bit, ou seja: o sentido de giro entre dois elétrons ou a polarização vertical ou horizontal de dois fótons.

Mas, com a separação de fótons ou eletrons, manipulados por uma torrente de bits, causaria um efeito semelhante?  

Notar que a separação de fótons ou elétrons depende da aceitação do  conceito de "localidade", desconsiderado pelos defensores da louca física quântica.

Por outro lado, a admissão "pontual" quantica destrói a hipótese relativista,  baseado na expansão contínua e progressiva do espaço cósmico, ou do crescente volume de dados nele contido.

Durmam com um Big Bang desses...

Como provar uma negação? Podemos provar que homens e lobos existem, mas não podemos provar que lobisomens não existem! Filosoficamente é impossível.
O Teorema de Bell é matematicamente incompreensível, ao menos para a maioria dos mortais.

O Experimento dos Filtros Polarizados

(Tradução Automática)



Notem que os filtros são postos à frente de um objeto iluminado, isto é: não-luminoso; isso dificulta a observação do efeito. Abaixo (*1), apresentamos a demonstração teórica do efeito esperado.

Cruzar dois filtros de luz polarizados linearmente bloqueia a luz. Mas adicionar um terceiro filtro polarizador num ângulo diagonal permite que a luz passe novamente, mas apenas se o filtro diagonal ficar entre os dois polarizadores cruzados, e não se vier antes ou depois deles.

Há uma boa explicação da física aqui, onde fica claro que os filtros realmente interagem com os fótons, em vez de apenas ler passivamente sua polarização constante.
http://alienryderflex.com/polarizer/

Como a luz também é feita de fótons, como exatamente você pode interpretar o que um filtro faz com um fóton fica muito menos claro, e ideias simples como “Um fóton tem uma polarização” não correspondem mais à realidade – a polarização que você lê depende dos filtros você aplica. Paul Dirac usou esse experimento exato como um exemplo introdutório aos efeitos da mecânica quântica em seu livro de 1930
https://www.informationphilosopher.com/solutions/experiments/dirac_3-polarizers/

(*1) O experimento com filtros polarizados

Copyright 2004 Darel Rex Finley. Todos os direitos reservados. Este artigo, com ilustrações e aviso de direitos autorais intactos, pode ser distribuído gratuitamente para fins educacionais.

Ilumine a luz através de dois filtros polarizadores orientados a 90° entre si e nenhuma luz passa. Mas coloque um terceiro filtro entre eles, a 45° de cada um dos filtros existentes, e surpreendentemente - algumas luzes passam!

Este experimento popular é frequentemente descrito como “estranho”. Geralmente é apresentado no contexto da mecânica quântica, como um exemplo do “assustador” dos efeitos quânticos. Raramente, porém, o apresentador informa ao público que esta experiência pode ser explicada em termos muito simples de causa e efeito, sem referência à assustadora magia quântica ou algo parecido.

Vamos começar examinando o experimento padrão:



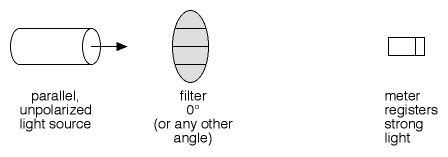
Figura 1

- Esquerda: fonte de Luz não polarizada;
- Centro: filtro polarizado horizontal (O°);
- Direita: Fotômetro indica luz intensa.

Na Figura 1, uma fonte de luz paralela e não polarizada é disparada através de um filtro polarizador, e a luz é fortemente registrada em um medidor de luz na outra extremidade.



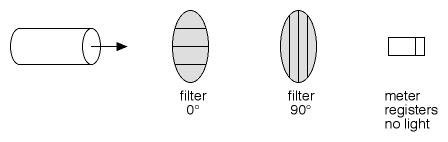
Figura 2: um filtro polarizado  vertical (90°) é adicionado após o filtro horizontal. O fotômetro não indica captura de luz.

Na Figura 2 é introduzido um segundo filtro, orientado a 90° em relação ao primeiro. Agora, nenhuma luz passa.


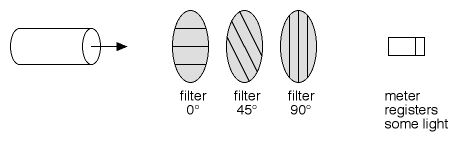
Figura 3: entre o filtro horizontal e o filtro vertical é adicionado um filtro diagonal(45°). Nessa condição, o fotômetro indica a captura de uma certa quantidade luz.

Na Figura 3, um terceiro filtro é colocado entre os dois primeiros, a 45° de cada um deles. De repente, o fotômetro registra uma quantidade significativa de luz, embora não tanto quanto na Figura 1.
Assustador!


Assombro e a palavra “filtro”

Por que esses resultados parecem assustadores? A razão é a aplicação incorreta da palavra “filtro”. Um filtro é comumente entendido como um dispositivo que tira alguns itens de um fluxo, enquanto deixa outros essencialmente intocados. Um bom exemplo de filtro é uma peneira – ela bloqueia objetos de um determinado tamanho, enquanto permite a passagem de objetos de outros tamanhos.

Figura 4



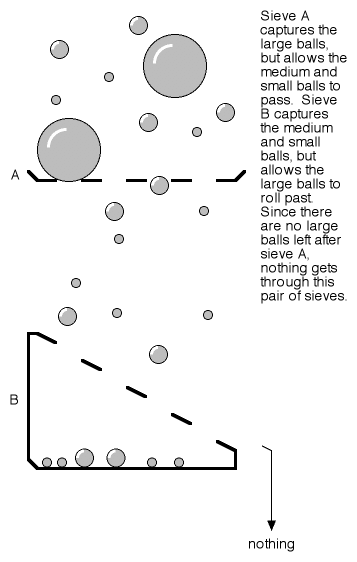
- A peneira A captura as bolas grandes, mas permite a passagem das bolas médias e pequenas;
- A peneira B captura as bolas médias e pequenas, mas permite que as bolas grandes passem;
- Como não restam bolas grandes depois da peneira A, nada passa por esse par de peneiras.

Mais:

Teorema de Bell
https://pt.wikipedia.org/wiki/Teorema_de_Bell

Paradoxo EPR
https://pt.wikipedia.org/wiki/Paradoxo_EPR

Citação e Reflexões sobre o Experimento da Postagem Anterior

Figura 3: entre o filtro horizontal e o filtro vertical é adicionado um filtro diagonal(45°). Nessa condição, o fotômetro indica a captura de uma certa quantidade luz.

Quando é adicionado um filtro diagonal entre os filtros horizontal e vertical, dependendo do material empregado, é de se esperar (ou desesperar  ) que possa ocorrer reflexão de ondas entre o primeiro e segundo filtros e a consequente formação de ondas estacionárias entre eles. Em outras palavras, a luz bate e rebate entre o primeiro e segundo filtros antes de que toda essa energia se transforme em calor. Nessa confusão estabelecida poderá ocorrer a torção do eixo em  -45 ou +45 graus das ondas polarizadas, de modo que muitas delas consigam passar do segundo para pelo terceiro filtro, ou até mesmo voltar para a fonte luminosa (esquerda) de luz ordinária.


"Não são tanto as coisas que não sabemos que nos metem em confusões.
São as coisas que pensamos que sabemos."

Contraponto de Millôr Fernandes:
"O mal das encrencas é que elas começam bem devagarinho."

"Use a estatística como o bêbado utiliza o poste, mais pelo apoio do que pela luz.   "

fonte:
https://www.inf.ufsc.br/~marcelo.menezes.reis/citar.html

Jonas Paulo Negreiros escreveu:Citação e Reflexões sobre o Experimento da Postagem Anterior

Figura 3: entre o filtro horizontal e o filtro vertical é adicionado um filtro diagonal(45°). Nessa condição, o fotômetro indica a captura de uma certa quantidade luz.

Quando é adicionado um filtro diagonal entre os filtros horizontal e vertical, dependendo do material empregado, é de se esperar (ou desesperar  ) que possa ocorrer reflexão de ondas entre o primeiro e segundo filtros e a consequente formação de ondas estacionárias entre eles. Em outras palavras, a luz bate e rebate entre o primeiro e segundo filtros antes de que toda essa energia se transforme em calor. Nessa confusão estabelecida poderá ocorrer a torção do eixo em  -45 ou +45 graus das ondas polarizadas, de modo que muitas delas consigam passar do segundo para pelo terceiro filtro, ou até mesmo voltar para a fonte luminosa (esquerda) de luz ordinária.


"Não são tanto as coisas que não sabemos que nos metem em confusões.
São as coisas que pensamos que sabemos."

Contraponto de Millôr Fernandes:
"O mal das encrencas é que elas começam bem devagarinho."

"Use a estatística como o bêbado utiliza o poste, mais pelo apoio do que pela luz.   "

fonte:
https://www.inf.ufsc.br/~marcelo.menezes.reis/citar.html

Advogados conhecem muito bem essa lei:



Essa é uma lição que aparentemente os quânticos ainda não aprenderam !