Albrandt - Atração Eletrostática

Não está na hora de corrigir um antigo erro? - Parte I
Roman Albrandt

Este trabalho é sobre fenômenos eletrostáticos conhecidos desde a antiguidade.
Não se trata de uma nova teoria que virá substituir as já existentes a respeito,
mas tão somente mostrar que os fenômenos eletrostáticos poderão ser
estudados e interpretados sob um novo ponto de vista. Pretendemos mostrar
que mesmo não aceitando as forças elétricas de repulsão, todos os fenômenos
eletrostáticos são explicados igualmente bem. Tanto assim que a lei de Coulomb,
bem como os resultados obtidos dela, não perdem o seu valor.
Não nos aprofundaremos ao ponto de tentar explicar os fenômenos sub-atômicos,
consequentemente àqueles ligados com as partículas elementares.
Nos restringiremos a corpos macroscópicos eletrizados.

A eletrostática é, sem dúvida, o mais antigo ramo da Eletricidade. O caráter
científico desta ciência foi dado quando, a cerca de 200 anos, foi estabelecida
a Lei de Coulomb. As experiências realizadas mais tarde para a construção da
Lei de Coulomb nunca tiveram a pretensão de mostrar novas teorias ou buscar
novos caminhos, mas se restringiram ao aspecto puramente didático e às
explicações a respeito dos fenômenos eletrostáticos sempre se baseavam na
formulação Coulombiana.

Novos estudos mais recentes, entretanto, mostram contradições entre a ciência
moderna e as conclusões baseadas na teoria de Coulomb. Ao estabelecer a
expressão da força Coulombiana entre duas cargas q1 e q2 de mesma
polaridade ou de polaridades diferentes separadas de uma distância r,

F = [q1 x q2/r^2] x constante K (1)

Coulomb, apesar de não ter ideia à respeito da natureza das cargas elétricas,
estabeleceu que as cargas da mesma polaridade se repeliam e aquelas de
cargas opostas se atraíam.

Pela observação de forças atrativas e repulsivas entre corpos, criou-se a
hipótese de que havia dois tipos de eletricidade: a "positiva" e a "negativa".
Estas eram suficientes para explicar os fenômenos observados.

Meio século depois surgiram os trabalhos de GAUSS sobre campos elétricos.
Com essa teoria, muitos abandonaram a ideia de "ação à distância" e ficaram
com a teoria dos campos. Com base na teoria dos campos determinou-se
onde fica armazenada a energia do campo elétrico. Entretanto, nessa mesma
época não se tinha uma ideia clara do que seria carga elétrica, e nem do
processo de eletrização.

Somente no início do século XX, após os trabalhos de RUTERFORD E BOHR,
chegou-se a uma compreensão da estrutura eletrônica dos materiais e,
consequentemente, uma explicação clara do significado de carga elétrica.

Hoje em dia, entendemos a corrente elétrica de condução como o movimento
de elétrons num condutor. E, corpos eletrizados são aqueles que têm seu
equilíbrio interno rompido [1]. O corpo que apresenta uma deficiência de
elétrons, tem um número maior de prótons e, consequentemente, dizemos
que trata de um corpo eletrizado positivamente. Por outro lado, o corpo que
apresenta um excesso de elétrons, é um corpo que dizemos estar eletrizado
negativamente.
Em ambos os casos, nos corpos carregados eletricamente com cargas elétricas
de polaridades opostas existem cargas elementares positivas (prótons) e cargas
elementares negativas (elétrons).

A diferença entre os corpos eletrizados com polaridades diferentes é somente
quantitativa e não qualitativa. Assim sendo, não devemos pensar em dois tipos
de eletricidade no sentido antigo. Partimos da premissa que só existe uma
espécie de eletricidade, que é determinada pela carga elétrica do elétron, isto
é, do tipo negativo. A quantidade desta, determina a polaridade de eletrização
de um corpo. A "eletricidade positiva" ou "eletricidade negativa" não existem,
também no ramo da eletrodinâmica. Só existe um tipo de eletricidade (aquela
determinada pelos elétrons) e o processo de eletrização nada mais é que a
transferência de elétrons de um corpo para outro [2]. Deste modo, quando ocorrer
a eletrização entre dois corpos, o doador de elétrons fica carregado
positivamente e o receptor, negativamente. No caso acima, aparece um campo
elétrico entre os corpos, onde existe uma energia armazenada, devido ao
processo de carga.


A explicação do fenômeno de eletrização dada acima está ligada aos fatos
cuja sequência lógica é a seguinte:

a)
Para carregar eletricamente um corpo é indispensável a existência de
outro corpo. Um corpo eletricamente carregado (frequentemente mencionado
nos livros de ensino) não pode existir e não existe na realidade.
Esse segundo corpo, que é parte do processo de carga, chamaremos de "corpo
componente" do nosso corpo carregado. Um desses corpos é doador e o outro
receptor de elétrons;

b)
Como a quantidade de elétrons determina o valor da carga transmitida, os
valores absolutos das cargas recebidas pelos corpos-componentes devem ser
obrigatoriamente iguais.

Então, a fórmula de Coulomb, no caso de existirem somente dois corpos, deveria ter a forma:

F = [q^2/r^2] x constante K (2)

c)
Não podem existir dois corpos com cargas de mesma polaridade, se existem
somente entre esses dois corpos e nada mais. Deve existir um outro corpo
(um terceiro) que fornece ou recebe elétrons.


Quando na mesa do laboratório carregamos eletricamente uma esfera metálica,
por exemplo, positivamente, tiramos uma quantidade de seus elétrons e
transferimos para o corpo-componente terra. Assim nossa esfera metálica
torna-se carregada positivamente e o ambiente (a mesa, as paredes, o teto e
todas as coisas ao redor) torna-se carregado negativamente.[3]

Aparece, também, um campo elétrico entre a esfera e todos os objetos ao redor
dela, onde está armazenada a energia gasta durante o processo de transferência
de elétrons. Mesmo quando os objetos do ambiente são afastados da nossa esfera
numa distância bem grande, o ambiente, como corpo-componente, não deixa de
existir e fica carregado (no nosso exemplo, negativamente), sendo ligado pelas
linhas de força do campo elétrico com a esfera.


[1] Physics for College Students - A. Knowton - pag. 229
[2] Teoria da Eletricidade - A. Martignoli - pág.29.
[3] Fundamental Principles of Physics - H. Heil & W. Bennet - pág. 435

O texto transcrito nessa postagem é de uma matéria publicada no Jornalzinho
Mackenzie, de novembro de 1978.

Fim da Primeira Parte

Não está na hora de corrigir um antigo erro? - Parte II

Roman Albrandt

Quando na mesa do laboratório carregamos eletricamente uma esfera metálica,
por exemplo, positivamente, tiramos uma quantidade de seus elétrons e transferimos para o corpo-componente terra. Assim nossa esfera metálica torna-se carregada positivamente e o ambiente (a mesa, as paredes, o teto e todas as coisas ao redor) torna-se carregado negativamente.

Aparece, também, um campo elétrico entre a esfera e todos os objetos ao redor dela, onde está armazenada a energia gasta durante o processo de transferência de elétrons. Mesmo quando os objetos do ambiente são afastados da nossa esfera numa distância bem grande, o ambiente, como corpo-componente, não deixa de
existir e fica carregado (no nosso exemplo, negativamente), sendo ligado pelas linhas de força do campo elétrico com a esfera.

Quando todos os objetos do ambiente são afastados para bem longe, podemos imaginar o ambiente como uma grande esfera vazia de raio R, que envolve nossa esfera metálica (com raio r) concentricamente (fig.1).



O importante papel do ambiente aqui descrito fica mais claro que nos outros livros. O campo elétrico entre esses dois corpos-componentes (a esfera metálica "a" e a esfera vazia "b" que simboliza o ambiente, é formado neste caso, pelas
linhas de força, as quais saem radialmente da superfície da esfera metálica "a" e terminam na superfície interna da esfera ambiente "b".

A energia armazenada dentro desse campo é:

W = C x U^2 (3)

onde:

U é o potencial da esfera "a" em relação ao ambiente "b";
C é a capacitância entre as duas esferas "a" e "b".

Cada parcela da superfície da esfera "a" sofre a força de atração pelas partes correspondentes da superfície "b" do ambiente. Mas a esfera "a" em geral não sofre nenhuma força, porque o campo elétrico ao redor dela é um campo completamente simétrico, com a soma vetorial de todas forças elementares igual a zero.

Se, por qualquer motivo, o campo elétrico ao redor da esfera "a" deixa de ser simétrico, a soma vetorial de todas as forças elementares não será mais igual a zero e a esfera sofrerá uma força de atração F de sentido correspondente ao vetor da soma vetorial. Se a esfera "a" tem a possibilidade de ser deslocada
de d1, será executado o trabalho:

dW = F x d1 (4)

É importante notar que este trabalho pode ser executado exclusivamente pela parte de energia W armazenada no campo elétrico entre a esfera "a" e o ambiente "b". Não existe nenhuma outra fonte de energia para esse trabalho.

Um campo elétrico assimétrico ao redor do corpo carregado aparece, por exemplo, quando perto de nossa esfera "a" colocamos uma outra esfera "c" de mesmo potencial U em relação ao ambiente (+).

Neste caso, a superfície da esfera, do ambiente "b" torna-se dividida em duas partes (fig.2)




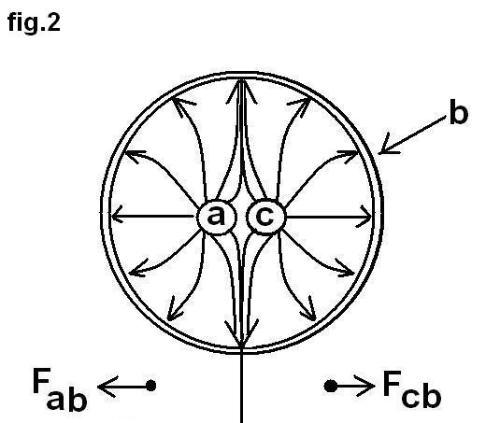
Cada uma das partes serve como corpo-componente para a esfera correspondente.
Assim aparecem dois campos elétricos assimétricos, cada esfera fica atraída pela parte da superfície ambiente "b" e as esferas afastam-se mutuamente.

O trabalho mecânico, realizado com este afastamento mútuo pode ser feito exclusivamente por conta da energia armazenada no espaço entre as esferas e o ambiente. Então, o fenômeno do afastamento mútuo das duas esferas "a" e "c" com as cargas de mesma polaridade explica-se logicamente sem a necessidade
de presumir a existência de algumas "forças de repulsão" entre as esferas.

A noção de força de repulsão foi introduzida na eletrostática no século 18 sem o conhecimento da existência dos campos elétricos portadores de energia, e sem perceber a importância dos campos elétricos entre os corpos carregados e o ambiente.

Foi uma única possibilidade de explicar o fenômeno de afastamento mútuo de duas cargas da mesma polaridade naquela época. Agora podemos constatar que não existe nenhuma justificativa física para o aparecimento de qualquer força entre os corpos de mesmo potencial, porque não existe nenhum campo elétrico comum entre eles, cuja energia possa executar trabalho de repulsão.

Somente a influência do ambiente que é o corpo-componente para ambos os corpos carregados, e que é ligado com eles pelos campos elétricos comuns, pode provocar esse fenômeno.

Fim da segunda parte.

Não está na hora de corrigir um antigo erro? - Parte III (Final)
Roman Albrandt

Uma experiência muito simples pode comprovar que as forças de atração pelo ambiente estão longe de ser insignificantemente pequenas. Elas são comparáveis com as forças de atração entre dois corpos colocados um perto do outro (fig.3).



Notamos que esta segunda esfera "c" é o terceiro corpo carregado, como já foi dito anteriormente.

Nota: a esfera "a" passa a ser denominada "1"; a esfera "c" passa a ser denominada "2".

Quando o cursor do reostato "R" está na posição "a", as esferas ficam mutuamente atraídas, como deveria acontecer conforme as regras de Coulomb, por terem cargas de polaridade diferente.

Deslocando-se o cursor do reostato no sentido da posição "b", reforçamos os campos elétricos entre as esferas. Quando as forças de atração entre as esferas "1" e "2" e o ambiente ficam mais fortes do que a força de atração entre elas, (o cursor do reostato na posição "b", as esferas afastam-se mutuamente, apesar de uma força de atração entre elas, que não pode de repente se transformar em uma força de repulsão.

CONCLUSÃO

A aparente contradição de nossa apresentação dos fenômenos eletrostáticos com a
costumeira (isto é, "clássica") explica-se pelo fato que esta última tem origem nos trabalhos dos físicos do século 18. Apesar do enorme progresso em todos os ramos da Física durante os últimos séculos, o capítulo de Eletrostática, com suas experiências, está apresentado até hoje na maioria dos livros de ensino numa
forma obsoleta de Física Pré-Eletrônica. Ainda fala-se de duas espécies de eletricidade: positiva e negativa. Fala-se de "cargas isoladas" e sobre outras coisas não aceitáveis para a física moderna, a Eletrônica.

Saindo de posições errôneas, a Física dos séculos passados chegou a algumas conclusões também não aceitáveis. Uma delas é o aparecimento das  "forças de repulsão". Como é conhecida, estas forças aparecem somente entre cargas de mesma polaridade.

Sabemos que a existência de cargas da mesma polaridade é impossível se apenas existem estas cargas e não outras. Para carregar dois corpos com a mesma polaridade é indispensável a presença de mais um corpo, o terceiro, ou seja, receptor ou doador de elétrons.

Então, é inevitável o aparecimento das forças elétricas entre os três corpos carregados. O problema torna-se, naturalmente, mais complicado e não pode ser resolvido para as "forças de repulsão" pela simples aplicação da fórmula de Coulomb.

Comentários do forista

Não encontrei nada na rede sobre esse interessante trabalho do prof. Albrandt.

É difícil imaginar as consequências dessa visão no mundo subatômico, nos quais as "forças de repulsão Coulombianas" ainda são consideradas!

A matéria foi publicada em 1978... Fico pensando como a Física é tão "conservadora" .

O experimento de Coulomb e Cavendish são muito semelhantes.
Cavendish usou um feixe de luz em seu experimento.

Embora Newton imaginava uma raio de luz como um feixe corpuscular, será que a pressão do feixe sobre o espelho foi considerado?

Nem Newton ou Cavendish não conheciam o efeito fotoelétrico.

Mais:
https://fisica2100.forumeiros.com/t1932p20-a-gravidade-no-seculo-21#12861